nonogram安卓版

nonogram安卓版是一款操作简单易上手的休闲闯关游戏，玩家能够借助这款游戏锻炼自己的大脑，适合不同年龄段的玩家体验，轻松有趣的游戏氛围让人沉浸其中，再加上舒缓的音乐和音效，非常值得一试，游戏包含海量关卡，每个关卡的设计都独具特色，十分好玩。

nonogram安卓版玩法

无论是数字类还是文字类的纵横游戏都十分好用，想必你也很熟悉了，这类游戏的玩法确实很容易让人上瘾。

多种主题拼图等待您去挑战，不要忘了领取成就奖励

5种挑战模式，选择最适合您的数织游戏难度等级

轻松愉快的背景音乐，能使自己快速放松下来

nonogram安卓版优势

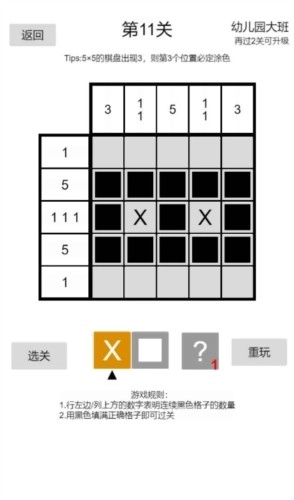
5种挑战模式，选择最适合您的数织游戏难度等级。

轻松愉快的背景音乐，能使自己快速放松下来。

这里有多种主题的拼图等待您来挑战，别忘了领取相应的成就奖励哦。

这是一个简单轻松的游戏世界，我们的游戏上手容易，操作简单，但想要精通却颇具挑战。

nonogram安卓版新手攻略

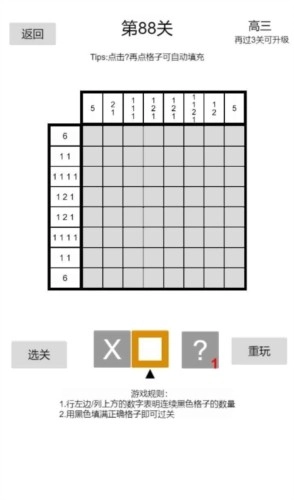
本系列中的简称及其说明

排：行/列

垂直：与排的方向垂直。

从k排起始的m×n区块：在未特别指明的情况下，一般指代游戏里所有排的整体集合。它也可用来描述一个矩形区域，这里的m代表行数，n代表列数。

场地格：初始状态的格子，存在在游戏的区块中。

第x行格：从任意一边开始数的第x个场地格

第x个数字：从任意一边开始数第x个数字

数字x的正格：是指必然存在黑块的格子，并且这个场地格肯定属于数字x图形的组成部分。

负格：一定无黑块的格子

数字x的位：数字x所可能代表的场地格

第一章：数字的位与数字的位的确定化

1-1概述

在数织时，我们始终要处理一些位置模糊的区域。借助这些区域与各个区块之间的关联，我们能够明确其中一部分的精准位置，进而一步步推导出完整的图像。

数字的准确位置通常能通过一排的格数和数字来推导，偶尔也会用到已确定的正格与负格，只有极少数关卡需要同时参考两排以上的信息。这让它的难度不会太高，本系列旨在帮助您从刚入门的新手快速成长为能推理大多数图形的高手。

注：以下所有定理与方法中我们将把负数看为零。

1-2 推演基础

怎样才能借助推演来明确精准的位置呢？我们不妨先提出一条极为简单的定理。

如果一排里只有一个数字，那么这一排中那些不属于数字的场地格就全都是负格。(1-2-1)

这条定理无需证明即可成立，也可以看作是数字位定义的另一种表述方式。

根据这条公理，我们能够发现，要想明确一个数字的精确位置，关键在于把它的位数缩减到不能再缩减的程度。而交叉排列与单一排列的限制条件，能够助力我们减少数字的位数。

我们来看一个简单的例子。

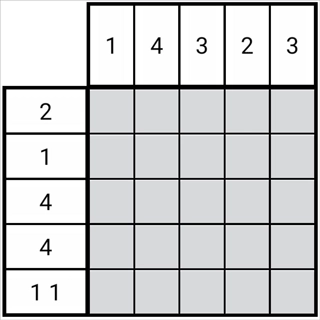
图1-2-1

如图所示，每一排的黑块在规则限定下仅存在有限种分布形态，这些分布形态被称作分布可能。

图中第二列存在两种分布情况，这两种情况之间有部分重叠区域，从图中能够发现，处于这个重叠区域内的格子必然是正格。

同理，图中第三列存在三种可能的分布情况，而这三种分布情况之间也有一个公共的区域，也就是第三列的第三格。所以，这个格子必然也是正格。

更普遍地说，在一排所有可能的分布情况里，始终存在黑块的格子被称为正格。

如果一个排里存在一个正格，并且这个正格里只有一个数字，那我们可以把它当成“固定”住这个数字所在位置的“钉子”；而这个位置能够在它的左右两侧“变动”，或者说增加格的数量，以此来推导出所有可能的分布情况。

同时，当两个正格将某个数字的位置固定住时，它们之间的部分也必然会被确定为正格。我们同样能够借助数学语言，把这一规律转化为如下的表述：

若某一排里只有一个数字，并且已经明确第m行的格子和第n行的格子都是正格，那么第i行的格子也为正格。这里的i属于这样的正整数集合：i是满足m≤x≤n或者n≤x≤m的正整数x。(1-2-2)

然而，由于数字数值大小的关联，一个数字的位会在正格的两侧增加特定数量的格数。这种增加不能超出数字既定的范围，所以我们从数学层面展开推导。

假设一排中仅存在一个数字k，第m行格和第n行格均为已知的正格，并且满足m≧n。根据式1-2-2可以推断，它们之间的所有格子都是正格，这些正格一共占据了(m-n+1)个格子。由此可知，在左右两侧还能增加的格子数量为k减去(m-n+1)。因此，从两端各增加相应数量的格子就能得到该数字的所有位置。也就是说，从第n减去[k-(m-n+1)]行格到第m加上[k-(m-n+1)]行格的范围，都是数字k的位置所在。经过整理后可以得出：

若某一排中存在唯一的数字k，且第m行格与第n行格均为正格（其中m≧n），则该数字的位置范围是从第(-k+m+1)行格至第(k+n-1)行格。(1-2-2)

1-3边缘法

我们之前提到过，数字可以对位形成限制，实际上，还有一种因素同样能起到限制作用，那就是场地格的边缘。场地格边缘之外显然无法存在位，特别是第一个数字，它往往离场地格的边缘最近，因此很容易受到限制。所以，我们有必要探讨边缘的相关情况。

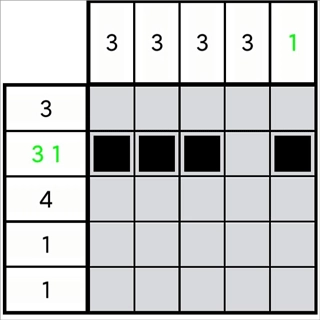
图1-3-1

如图1-3-1所示，很明显图中第1列的位无法向上增加两格，但它确实符合定理(1-2-3)的前置条件。我们不妨换个思路：既然不能向上增加，那就必须向下增加。所以，向上不能增加的格数，就要通过向下增加相同的格数来弥补。

设一排中存在且仅存在一个数字m，并且已知第n行的格子是正格，同时满足m＞n这一条件。那么，这一排无法再增加的格子数量为(m - n)格。若把这些数量的格子沿着向下的方向进行增加，就能得到：

若某一排中存在且仅存在一个数字m，同时第n行的格子为正格，且满足m大于n，那么对于所有属于正整数集合且处于区间[n，m]内的i而言，第i行的格子均为正格。(1-3-1)

观察这个定理，当m＞n时，意味着该数字对应的位必然覆盖了从第1行格到第n行格的范围。倘若我们将其假定为第一个数字，不难发现这个定理依旧是成立的。由此可得：

若某一排第n行的格是正格，并且该正格的第一个数字为m（m>n），那么对于满足i∈[n，m]且i为正整数的所有i，第i行的格均为正格。(1-3-2)

当单个数字处于边缘位置时，它的状态不会有太大改变，不过，要是我们探讨的是一整排数字的情形，那结果又会是怎样的呢？

这里我们介绍一种方法——整体法：在确定两个相邻数字的位时，可将这两个数字视为一个整体数字来处理，它们的位也相应看作这个整体数字的位。这种处理方式能简化运算过程，还能帮助我们分析连续排列的整体情况。

我们能够留意到这样一个现象：当由多个数字构成的整体位于边缘位置时，会呈现出一种独特的排列方式——数字-空格-数字-空格。这种排列方式将数字所占据的空间压缩到了极致，我们把这种整体处于边缘的排列状态称作边缘状态。

当一个实心物体在直道内滑动时，不难想象，它的投影与初始投影的公共部分会逐渐变小。所以，该物体所有运动瞬间投影的公共部分，其实和它处于边缘状态时投影的公共部分是一样的。基于这一点，我们能够得到：

没有负格的一排中，所有可能分布的公共部分由其边缘状态所决定。

不难发现，这样的描述乍看之下十分完美，实则存在一处小瑕疵——当多个数字构成一个整体时，它们所占的空间能够伸缩变化，而边缘状态必然是最短的。不过话说回来，我们距离完善它其实只差最后一步了。

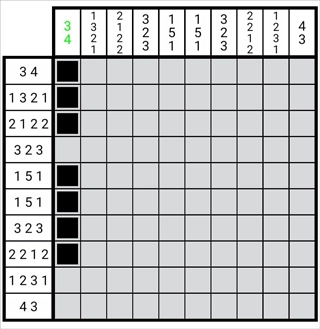
图1-3-2

如图所示，我们能够在第一列自上而下构建一个图形，该图形呈现第一列所有数字整体的边缘状态，此时这一列从下往上数总共有2个空格。这表明该图形中每个数字的位都可以向下延伸两格，因此我们将图形里对应每个数字的图形自上至下缩减两格，具体如图所示。

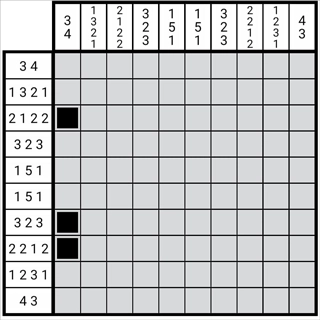
图1-3-3

通过这种方式，我们便能确定该列的正格。此方法生成的最终图形，其数字位与原始图形是相互对应的。在此我们略去了对边缘状态的检查——边缘状态的重叠无关紧要，关键在于重要数字与图形需严格一一对应。由于图形可长可短，但任一图形的活动范围都存在限制，这种限制恰好由图形自身长度与区块长度共同决定。只有当图形与数字达成一一对应时，该方法才具备实际意义。据此，我们也反向推导出了二者必然一一对应的原因，并且可以将这一性质应用到解题过程中。这也为后续第二章的内容做了部分铺垫。

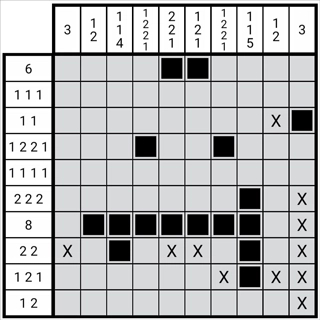
图1-3-4

如图所示，图中第七列第七行的位置，是通过该方法确定的第七列第3个数字2；依据位置关系的对应性，第4个数字1必然位于第七列第十行。

综上所述，我们能够归纳出一种快速判定正格的方法：首先从一排的第一行格起，按顺序绘制出上述的数字-空格图形，接着从起始方向减去最后剩余的空格数量，若结果为负数则视为零。最终得到的图形必然是正格。而且这些图形与原图形的位置关系是对应的，同时也是运用第一章所有方法所能获取的最多正格，这种方法被称作边缘法。

nonogram安卓版优势

挑选最契合自身的难度，从基础起步慢慢提升游戏里的难度等级

借助像素化逻辑谜题挖掘更多线索，解开其中潜藏的图像。

这款纵横数字游戏上手简单，一旦开始玩就会让人特别上瘾。

舒缓的自然音效与轻柔的背景音乐交织，能迅速安抚躁动的心神，让内心重归宁静。

nonogram安卓版描述

创新拼图新体验：nonogram安卓版把数字推理和艺术精妙融合，让玩家享受到前所未有的解谜乐趣。

精心设计的关卡体系：拥有数百乃至上千个风格各异的关卡，难度循序渐进，助力玩家持续突破自我。

精美的图案收集：玩家完成关卡后，便能解锁并收集各类精美的图案，以此展现自身的智慧与个性。

游戏支持免费畅玩，全程打扰，让玩家可以尽情沉浸在纯粹的游戏体验里。

小编点评：